Deterministic Parity Automata – What Are They Good For?
Deterministic parity (word) automata are often introduced as the simplest deterministic automaton model for words of infinite length that can capture all  -regular acceptance conditions. As such, they have an important role in formal methods and are useful in control applications (when working with
-regular acceptance conditions. As such, they have an important role in formal methods and are useful in control applications (when working with  -regular specifications).
-regular specifications).
Most scientific papers (and lectures) that use parity word automata do not give an example that helps the reader to gain an intuition on why they are defined in the way they are and how they can be used to encode  -regular specifications. The role of this document is to provide an example that should help to understand them in a better way. After going through the definition of a parity automaton, we construct multiple automata that encode reactive system specifications and finally discuss what such automata can be used for.
-regular specifications. The role of this document is to provide an example that should help to understand them in a better way. After going through the definition of a parity automaton, we construct multiple automata that encode reactive system specifications and finally discuss what such automata can be used for.
Definition
Before we can give an example, we need to define what we are talking about.
Given a set  , we denote by
, we denote by  the set of infinite sequences all of whose elements are in
the set of infinite sequences all of whose elements are in  .
A deterministic parity word automaton is defined as a tuple
.
A deterministic parity word automaton is defined as a tuple  with the finite set of states
with the finite set of states  , the finite alphabet
, the finite alphabet  , the transition function
, the transition function  , the initial state
, the initial state  , and the coloring function
, and the coloring function  .
.
A parity word automaton  defines a language
defines a language  over words
over words  . Given such a word,
. Given such a word,  induces a run
induces a run  with
with  and for every
and for every  , we have
, we have  . We have
. We have  if and only if
if and only if  is accepting. We say that
is accepting. We say that  is accepting (and hence,
is accepting (and hence,  is accepted) if and only if the highest value that occurs infinitely often in the sequence
is accepted) if and only if the highest value that occurs infinitely often in the sequence  is even.
is even.
Remarks:
The definition of the parity acceptance condition varies slightly between the publications. In publications that contain new game-theoretic results, an infinite run is often defined to be accepting if and only if the lowest color occurring infinitely often along it is even. Likewise, a run can be defined to be accepting if and only if the lowest or highest color occurring infinitely often along it is odd. All of these possible definitions are equivalent, as we can easily translate a coloring function to another coloring function  for sufficiently high
for sufficiently high  to switch between whether we are interested in the highest or the lowest color. Likewise, when switching between oddness and evenness for the highest or lowest color occurring infinitely often along a run, we just need to add
to switch between whether we are interested in the highest or the lowest color. Likewise, when switching between oddness and evenness for the highest or lowest color occurring infinitely often along a run, we just need to add  to all color values.
to all color values.
Colors are also often called priorities in the literature.
Sometimes, deterministic automata do not need to have successor states for every combination of predecessor state and alphabet symbol. If no transition is present, the automaton rejects a word. The model above is equivalent in the sense that we can always introduce a rejecting sink state to which we can divert finite-length runs that should be rejecting.
In this document, we use the above definition (highest color should be even) as it seems to be most common in the area of reactive synthesis, from which we draw the example given below.
A Simple Specification for a Simple Reactive System
We consider an example in which a deterministic parity word automaton is to be constructed that encodes a specification over a reactive system. A reactive system reads, in every of its computation cycles, the values of its input propositions and writes the values of its output propositions. The propositions of the reactive system that we are concerned with in this example are depicted in the following image:
![text{ begin{tikzpicture} draw[fill=black!30!white,rounded corners=0.5cm] (0,0) rectangle (4,2); draw[thick,->] (2.0,3) node[above] {makemath{r}} -- (2.0,2); draw[thick,->] (1.0,0) -- (1.0,-1) node[below] {makemath{g}}; draw[thick,->] (3.0,0) -- (3.0,-1) node[below] {makemath{mathit{init}}}; node at (2,1) {begin{tabular}{c}ReactiveSystemend{tabular}}; end{tikzpicture} }](eqs/6ltzeyilj2y7c-280.png)
A reactive system operates in steps. In every step, the system reads the values of its input propositions and writes the values of its output propositions. The system has no designated time of going out of service, so the traces of the system that collect the input and output in every computation cycle are infinitely long. An example trace of the system is:

In every tuple, the upper-most element represents the value of  , while the other elements represent
, while the other elements represent  and
and  . A specification now categorizes traces into those that satisfy it and those that do not. Typically, specifications are used to check some implementation of a reactive system for correctness or as a starting point to the automatic synthesis of reactive system implementations.
For a specification given as a parity automaton, all traces that induce accepting runs in the automaton are said to satisfy the specification.
. A specification now categorizes traces into those that satisfy it and those that do not. Typically, specifications are used to check some implementation of a reactive system for correctness or as a starting point to the automatic synthesis of reactive system implementations.
For a specification given as a parity automaton, all traces that induce accepting runs in the automaton are said to satisfy the specification.
Let us start with a simple automaton that encodes that if  occurs infinitely often in a trace, then also
occurs infinitely often in a trace, then also  needs to occur infinitely often in the trace.
needs to occur infinitely often in the trace.
![text{ begin{tikzpicture} node[draw,shape=circle,fill=blue!20!white] (a) at (0,0) {makemath{q_0}}; node[draw,shape=circle,fill=blue!20!white] (b) at (2,0) {makemath{q_1}}; node[draw,shape=circle,fill=blue!20!white] (c) at (4,0) {makemath{q_2}}; draw[thick,->,bend left=10] (a) to node[above] {makemath{r overline{g}}} (b); draw[thick,->,bend right=70] (a) to node[below] {makemath{g}} (c); draw[thick,->] (c) to[loop right] node[right] {makemath{g}} (c); draw[thick,->] (b) to[loop above] node[above] {makemath{roverline{g}}} (b); draw[thick,->,bend left=10] (b) to node[above] {makemath{g}} (c); draw[thick,->,bend left=10] (c) to node[below] {makemath{r overline{g}}} (b); draw[thick,->,bend right=70] (c) to node[above] {makemath{overline{rg}}} (a); draw[thick,->,bend left=10] (b) to node[below] {makemath{overline{rg}}} (a); draw[thick,->] (a) to[loop left] node[left] {makemath{overline{rg}}} (a); draw[thick,->] (-0.6,0.6) -- (a); draw[thick,->,fill=black] (-0.6,0.6) circle (0.05cm); end{tikzpicture} }](eqs/gjh9nyuoh29tb-280.png)
The automaton has three states, where all states with the names  for some
for some  have color
have color  . All edges in the automaton are labeled by Boolean formulas that describes the trace characters under which the transition should be taken. So a
. All edges in the automaton are labeled by Boolean formulas that describes the trace characters under which the transition should be taken. So a  transition is taken if both
transition is taken if both  and
and  have
have  values in the trace.
values in the trace.
The automaton looks complicated, but is in fact quite simple. Whenever  holds on an element of a trace, the automaton switches to state
holds on an element of a trace, the automaton switches to state  . Whenever
. Whenever  holds, it switches to state
holds, it switches to state  , and whenever
, and whenever  holds, it switches to state
holds, it switches to state  .
.
Let us now analyze whether the automaton represents the specification that we want it to encode. By the definition of the automaton, we have that  is visited infinitely often if
is visited infinitely often if  occurs infinitely often along a trace. Since
occurs infinitely often along a trace. Since  is the highest color in the automaton, this means that the automaton accepts such a run. Since
is the highest color in the automaton, this means that the automaton accepts such a run. Since  is odd, the only other way for the automaton to accept is if state
is odd, the only other way for the automaton to accept is if state  is visited infinitely often, but states
is visited infinitely often, but states  and
and  are not. This means that eventually, states
are not. This means that eventually, states  and
and  are not visited any more. This happens if neither
are not visited any more. This happens if neither  nor
nor  appear infinitely often, in which case the specification is fulfilled.
If color
appear infinitely often, in which case the specification is fulfilled.
If color  is the highest color visited infinitely often, then we know by the structure of the automaton that
is the highest color visited infinitely often, then we know by the structure of the automaton that  appears infinitely often along a trace, but not
appears infinitely often along a trace, but not  . In this case, the trace is rightfully rejected.
. In this case, the trace is rightfully rejected.
Now does this specification make any sense in the real world? If we interpret  as a request signal and
as a request signal and  as a grant signal, then the specification tells us that if requests keep coming, a grant should eventually be issued. So the specification could be a part of the properties that some hardware arbiter should fulfill, but the specification is not complete yet.
as a grant signal, then the specification tells us that if requests keep coming, a grant should eventually be issued. So the specification could be a part of the properties that some hardware arbiter should fulfill, but the specification is not complete yet.
So let us now make it more complete.
Let us assume that the  signal should symbolize whether the system has been correctly initialized. The system is allowed to switch the signal from
signal should symbolize whether the system has been correctly initialized. The system is allowed to switch the signal from  to
to  a couple of times, but eventually, the signal must stay at a
a couple of times, but eventually, the signal must stay at a  level. This requirement comes in addition to the one that we already gave above.
level. This requirement comes in addition to the one that we already gave above.
Let us implement the additional specification part by modifying the parity automaton from above using intuition. We can do so by adding a state with a color of  that should be visited whenever
that should be visited whenever  was just observed to have a value of
was just observed to have a value of  . Thus, if
. Thus, if  does not at some point stay at
does not at some point stay at  , we have that the state with color
, we have that the state with color  is visited infinitely often, and hence the trace is rejected. Otherwise, a run of the automaton stays in the states that we already had in the automaton above. The new parity automaton looks as follows:
is visited infinitely often, and hence the trace is rejected. Otherwise, a run of the automaton stays in the states that we already had in the automaton above. The new parity automaton looks as follows:
![text{ begin{tikzpicture} node[draw,shape=circle,fill=blue!20!white] (a) at (-1,0) {makemath{q_0}}; node[draw,shape=circle,fill=blue!20!white] (b) at (2,0) {makemath{q_1}}; node[draw,shape=circle,fill=blue!20!white] (c) at (5,0) {makemath{q_2}}; node[draw,shape=circle,fill=blue!20!white] (d) at (2,-4) {makemath{q_3}}; % draw[thick,->,bend right=20] (a) to node[above right,pos=0.8] {makemath{overline{mathit{init}}}} (d); draw[thick,->,bend left=40] (d) to node[below left,pos=0.5] {*} (a); draw[thick,->,bend left=20] (b) to node[right,pos=0.8] {makemath{overline{mathit{init}}}} (d); draw[thick,->,bend left=30] (c) to node[below right,pos=0.8] {makemath{overline{mathit{init}}}} (d); % draw[thick,->,bend left=10] (a) to node[above] {makemath{{mathit{init}},r overline{g}}} (b); draw[thick,->,bend right=60] (a) to node[above,pos=0.4] {makemath{{mathit{init}},g}} (c); draw[thick,->] (c) to[loop right] node[right] {makemath{{mathit{init}},g}} (c); draw[thick,->] (b) to[loop above] node[above] {makemath{{mathit{init}},roverline{g}}} (b); draw[thick,->,bend left=10] (b) to node[above] {makemath{{mathit{init}},g}} (c); draw[thick,->,bend left=10] (c) to node[below] {makemath{{mathit{init}},r overline{g}}} (b); draw[thick,->,bend right=70] (c) to node[above] {makemath{mathit{init},overline{rg}}} (a); draw[thick,->,bend left=10] (b) to node[below] {makemath{mathit{init},overline{rg}}} (a); draw[thick,->] (a) to[loop left] node[left] {makemath{mathit{init},overline{rg}}} (a); draw[thick,->] (-1.6,0.6) -- (a); draw[thick,->,fill=black] (-1.6,0.6) circle (0.05cm); end{tikzpicture} }](eqs/4opumwptk3pbd-280.png)
It may look surprising at first that from state  , the automaton always transitions to
, the automaton always transitions to  . This is because it does not really matter where the transition goes to. If
. This is because it does not really matter where the transition goes to. If  maintains a value of
maintains a value of  at some point, then the automaton run eventually moves to the states representing the
at some point, then the automaton run eventually moves to the states representing the  and
and  values. On the other hand, if
values. On the other hand, if  infinitely often has a value of
infinitely often has a value of  , then state
, then state  is visited at least on every second occurrence of a trace element in which
is visited at least on every second occurrence of a trace element in which  has a value of
has a value of  , so the automaton rejects the word.
, so the automaton rejects the word.
The specification encoded by the automaton is still relatively simple. Real-world practical specifications consist of many more properties, and the resulting parity automata are much more complicated then. In particular, so-called safety properties are often added to practical specifications. These state that the system under design should never perform certain specified sequences of actions. Strenghtening a specification represented as a deterministic parity automaton by some safety property can be done without changing the number of colors in the automaton (provided that there was already at least one odd color in the automaton). Since safety properties are quite frequent in practical specifications, but non-safety properties are more rare, this means that parity automata for real-life specifications can often have few colors.
We want to explore this possibility by giving a complete specification for the above arbiter scenario. We write down all requirements that the reactive system should fulfill, and formalize them in linear temporal logic (LTL). While we will not define LTL here (as probably most readers that reached this point of this page will be familiar with it), and just give the translation of the English language specification parts to LTL.
If
 has a value of
has a value of  infinitely often along a trace, then
infinitely often along a trace, then  should have a value of
should have a value of  infinitely often along it.
infinitely often along it.The value of
 should eventually stay at
should eventually stay at 
Proposition
 may only have a value of
may only have a value of  if
if  had a value of
had a value of  for at least three steps before.
for at least three steps before.The system can never give two grants (
 ) in a row.
) in a row.The value of
 can only switch from
can only switch from  to
to 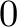 if
if  was
was 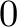 during the previous two steps of the trace.
during the previous two steps of the trace.
In LTL, these properties can be written as:
There are tools available to automatically translate LTL formulas into deterministic parity automata. One of them comes with the spot framework. For example, for spot 2.3.5, we can run the following command to compute a deterministic parity automaton for the conjunction of these five LTL properties:
ltl2tgba -G -D -S -d"avc" -f "([]<>r -> []<>g) & <>[]init & [](X X g -> init & X init & X X init ) & ! g & ! X g & [](! g | X ! g) & G(init & ! X init -> ! r & ! X r)" | dot2tex -f tikz
Note that the globally operator ( ) of LTL is written as [] in this command, while the finally operator (
) of LTL is written as [] in this command, while the finally operator ( ) is given as <>. The ltl2tgba tool of spot computed a parity automaton that looks as follows:
) is given as <>. The ltl2tgba tool of spot computed a parity automaton that looks as follows:
![enlargethispage{100cm} text{ scalebox{0.30}{ begin{tikzpicture}[>=latex',line join=bevel,] %% begin{scope} definecolor{strokecol}{rgb}{0.0,0.0,0.0}; pgfsetstrokecolor{strokecol} draw (732.5bp,2024.6bp) node {Fin(0) & (Inf(1) | (Fin(2) & Inf(3)))}; end{scope} node (24) at (660.0bp,1303.7bp) [draw,ellipse] {24 / {1}}; node (20) at (896.0bp,241.71bp) [draw,ellipse] {20}; node (21) at (742.0bp,1199.0bp) [draw,ellipse] {21 / {1}}; node (22) at (724.0bp,938.03bp) [draw,ellipse] {22 / {0}}; node (23) at (268.0bp,1087.9bp) [draw,ellipse] {23 / {0,1}}; node (1) at (125.0bp,1870.1bp) [draw,ellipse] {1}; node (0) at (279.0bp,1957.1bp) [draw,ellipse] {0}; node (3) at (736.0bp,1774.2bp) [draw,ellipse] {3 / {0}}; node (2) at (484.0bp,1591.3bp) [draw,ellipse] {2}; node (5) at (191.0bp,1591.3bp) [draw,ellipse] {5}; node (4) at (484.0bp,1678.3bp) [draw,ellipse] {4}; node (7) at (213.0bp,1303.7bp) [draw,ellipse] {7 / {0}}; node (6) at (94.0bp,1408.5bp) [draw,ellipse] {6 / {1}}; node (9) at (494.0bp,1199.0bp) [draw,ellipse] {9}; node (8) at (468.0bp,1504.3bp) [draw,ellipse] {8}; coordinate (I) at (279.0bp,2012.6bp); node (11) at (266.0bp,1009.8bp) [draw,ellipse] {11 / {1}}; node (10) at (724.0bp,1087.9bp) [draw,ellipse] {10}; node (13) at (525.0bp,750.66bp) [draw,ellipse] {13}; node (12) at (501.0bp,840.66bp) [draw,ellipse] {12}; node (15) at (668.0bp,339.07bp) [draw,ellipse] {15 / {2}}; node (14) at (597.0bp,33.234bp) [draw,ellipse] {14 / {1,2}}; node (17) at (1090.0bp,653.3bp) [draw,ellipse] {17 / {3}}; node (16) at (968.0bp,443.81bp) [draw,ellipse] {16 / {3}}; node (19) at (1188.0bp,548.55bp) [draw,ellipse] {19 / {1}}; node (18) at (785.0bp,144.34bp) [draw,ellipse] {18 / {1}}; draw [->] (13) ..controls (625.55bp,732.69bp) and (944.21bp,678.9bp) .. (17); draw (861.0bp,705.67bp) node {g & init & !r}; draw [->] (4) ..controls (510.62bp,1687.4bp) and (520.0bp,1684.9bp) .. (520.0bp,1678.3bp) .. controls (520.0bp,1674.1bp) and (516.15bp,1671.6bp) .. (4); draw (546.5bp,1678.3bp) node {!g & !init}; draw [->] (13) ..controls (634.44bp,760.12bp) and (1006.0bp,791.91bp) .. (1006.0bp,839.66bp) .. controls (1006.0bp,1679.3bp) and (1006.0bp,1679.3bp) .. (1006.0bp,1679.3bp) .. controls (1006.0bp,1728.0bp) and (847.18bp,1757.3bp) .. (3); draw (1046.5bp,1303.7bp) node {!g & !init & !r}; draw [->] (15) ..controls (649.83bp,260.3bp) and (621.66bp,139.74bp) .. (14); draw (670.5bp,196.71bp) node {g & init & r}; draw [->] (24) ..controls (689.52bp,1339.3bp) and (704.99bp,1360.4bp) .. (714.0bp,1381.6bp) .. controls (735.8bp,1432.8bp) and (756.64bp,1571.9bp) .. (762.0bp,1627.3bp) .. controls (765.72bp,1665.8bp) and (756.11bp,1709.4bp) .. (3); draw (793.5bp,1547.8bp) node {!g & !init & !r}; draw [->] (8) ..controls (473.46bp,1460.6bp) and (474.86bp,1411.0bp) .. (449.0bp,1381.6bp) .. controls (430.05bp,1360.0bp) and (406.75bp,1384.4bp) .. (387.0bp,1363.6bp) .. controls (349.39bp,1323.9bp) and (394.29bp,1285.6bp) .. (359.0bp,1243.8bp) .. controls (345.62bp,1228.0bp) and (330.21bp,1240.9bp) .. (316.0bp,1225.8bp) .. controls (291.58bp,1199.9bp) and (279.49bp,1160.9bp) .. (23); draw (407.5bp,1303.7bp) node {g & init & r}; draw [->] (22) ..controls (687.21bp,884.1bp) and (643.17bp,826.22bp) .. (595.0bp,788.16bp) .. controls (582.02bp,777.91bp) and (565.72bp,769.21bp) .. (13); draw (705.0bp,840.66bp) node {!g & init & !r}; draw [->] (10) ..controls (724.0bp,1044.9bp) and (724.0bp,1004.7bp) .. (22); draw (760.0bp,1009.8bp) node {!g & init & r}; draw [->] (4) ..controls (435.9bp,1663.0bp) and (369.85bp,1643.5bp) .. (314.0bp,1627.3bp) .. controls (280.97bp,1617.8bp) and (242.89bp,1607.0bp) .. (5); draw (404.0bp,1634.8bp) node {!g & init & !r}; draw [->] (20) ..controls (950.35bp,281.95bp) and (1055.9bp,355.16bp) .. (1153.0bp,398.94bp) .. controls (1177.6bp,410.04bp) and (1195.0bp,395.21bp) .. (1211.0bp,416.94bp) .. controls (1232.1bp,445.59bp) and (1219.3bp,487.24bp) .. (19); draw (1191.0bp,391.44bp) node {!g & init & !r}; draw [->] (9) ..controls (493.86bp,1259.7bp) and (491.93bp,1374.3bp) .. (477.0bp,1468.3bp) .. controls (476.56bp,1471.1bp) and (476.01bp,1473.9bp) .. (8); draw (528.0bp,1356.1bp) node {!g & init & !r}; draw [->] (24) ..controls (654.38bp,1246.4bp) and (643.41bp,1197.3bp) .. (611.0bp,1172.1bp) .. controls (552.65bp,1126.7bp) and (414.41bp,1204.9bp) .. (448.0bp,1139.1bp) .. controls (499.32bp,1038.5bp) and (627.45bp,976.73bp) .. (22); draw (484.0bp,1146.6bp) node {!g & init & r}; draw [->] (2) ..controls (478.63bp,1561.8bp) and (475.62bp,1545.8bp) .. (8); draw (515.0bp,1547.8bp) node {!g & init & !r}; draw [->] (I) ..controls (279.0bp,2010.4bp) and (279.0bp,1998.0bp) .. (0); draw [->] (5) ..controls (229.91bp,1611.5bp) and (273.75bp,1634.6bp) .. (307.0bp,1660.3bp) .. controls (324.91bp,1674.2bp) and (324.15bp,1683.8bp) .. (343.0bp,1696.3bp) .. controls (375.38bp,1717.8bp) and (386.47bp,1719.2bp) .. (424.0bp,1729.3bp) .. controls (521.16bp,1755.5bp) and (639.78bp,1766.7bp) .. (3); draw (383.5bp,1678.3bp) node {!g & !init & !r}; draw [->] (7) ..controls (276.97bp,1247.1bp) and (382.4bp,1157.7bp) .. (425.0bp,1139.1bp) .. controls (517.25bp,1098.8bp) and (638.54bp,1090.7bp) .. (10); draw (407.0bp,1199.0bp) node {g & init & !r}; draw [->] (14) ..controls (527.59bp,60.239bp) and (468.0bp,92.301bp) .. (468.0bp,143.34bp) .. controls (468.0bp,340.07bp) and (468.0bp,340.07bp) .. (468.0bp,340.07bp) .. controls (468.0bp,374.75bp) and (451.0bp,460.51bp) .. (451.0bp,495.18bp) .. controls (451.0bp,654.3bp) and (451.0bp,654.3bp) .. (451.0bp,654.3bp) .. controls (451.0bp,687.41bp) and (479.2bp,715.98bp) .. (13); draw (503.0bp,391.44bp) node {!g & init & !r}; draw [->] (4) ..controls (484.0bp,1648.5bp) and (484.0bp,1632.9bp) .. (2); draw (520.0bp,1634.8bp) node {!g & init & r}; draw [->] (21) ..controls (812.52bp,1196.0bp) and (891.42bp,1186.5bp) .. (880.0bp,1139.1bp) .. controls (861.71bp,1063.3bp) and (853.75bp,1039.4bp) .. (800.0bp,982.9bp) .. controls (788.2bp,970.49bp) and (772.11bp,960.52bp) .. (22); draw (912.0bp,1087.9bp) node {!g & init & r}; draw [->] (19) ..controls (1154.4bp,531.29bp) and (1142.7bp,526.01bp) .. (1132.0bp,521.68bp) .. controls (1109.3bp,512.55bp) and (1102.0bp,514.45bp) .. (1080.0bp,503.68bp) .. controls (1069.0bp,498.32bp) and (1067.6bp,494.73bp) .. (1057.0bp,488.68bp) .. controls (1039.1bp,478.49bp) and (1018.5bp,468.25bp) .. (16); draw (1118.0bp,496.18bp) node {!g & init & !r}; draw [->] (22) ..controls (842.29bp,920.57bp) and (1146.7bp,864.31bp) .. (1289.0bp,680.17bp) .. controls (1385.3bp,555.61bp) and (1388.0bp,497.5bp) .. (1388.0bp,340.07bp) .. controls (1388.0bp,340.07bp) and (1388.0bp,340.07bp) .. (1388.0bp,143.34bp) .. controls (1388.0bp,67.248bp) and (806.19bp,41.423bp) .. (14); draw (1415.5bp,496.18bp) node {g & init & r}; draw [->] (16) ..controls (1002.0bp,466.29bp) and (1015.0bp,476.74bp) .. (1024.0bp,488.68bp) .. controls (1053.5bp,527.9bp) and (1071.9bp,582.1bp) .. (17); draw (1104.0bp,548.55bp) node {g & init & !r}; draw [->] (6) ..controls (147.58bp,1397.1bp) and (191.24bp,1388.7bp) .. (229.0bp,1381.6bp) .. controls (308.07bp,1366.7bp) and (327.81bp,1362.8bp) .. (407.0bp,1348.6bp) .. controls (483.85bp,1334.8bp) and (573.97bp,1319.3bp) .. (24); draw (443.0bp,1356.1bp) node {g & init & !r}; draw [->] (18) ..controls (730.09bp,111.47bp) and (672.23bp,77.891bp) .. (14); draw (741.5bp,91.968bp) node {g & init & r}; draw [->] (19) ..controls (1171.2bp,512.72bp) and (1163.9bp,499.61bp) .. (1156.0bp,488.68bp) .. controls (1149.5bp,479.78bp) and (1146.1bp,479.07bp) .. (1139.0bp,470.68bp) .. controls (1119.5bp,447.79bp) and (1123.6bp,432.6bp) .. (1098.0bp,416.94bp) .. controls (1031.8bp,376.52bp) and (796.64bp,351.6bp) .. (15); draw (1175.0bp,443.81bp) node {!g & init & r}; draw [->] (23) ..controls (319.1bp,1041.4bp) and (362.28bp,1001.6bp) .. (397.0bp,964.9bp) .. controls (428.79bp,931.26bp) and (462.89bp,889.68bp) .. (12); draw (481.0bp,938.03bp) node {!g & init & r}; draw [->] (12) ..controls (509.28bp,809.31bp) and (513.68bp,793.17bp) .. (13); draw (553.0bp,795.66bp) node {!g & init & !r}; draw [->] (8) ..controls (503.74bp,1515.8bp) and (533.72bp,1526.2bp) .. (557.0bp,1540.3bp) .. controls (591.75bp,1561.4bp) and (671.99bp,1626.8bp) .. (695.0bp,1660.3bp) .. controls (711.14bp,1683.8bp) and (721.74bp,1714.4bp) .. (3); draw (720.5bp,1634.8bp) node {!g & !init & !r}; draw [->] (6) ..controls (133.48bp,1373.4bp) and (163.5bp,1347.5bp) .. (7); draw (197.0bp,1356.1bp) node {!g & init & r}; draw [->] (16) ..controls (1030.3bp,421.7bp) and (1094.0bp,391.44bp) .. (1094.0bp,340.07bp) .. controls (1094.0bp,340.07bp) and (1094.0bp,340.07bp) .. (1094.0bp,143.34bp) .. controls (1094.0bp,50.848bp) and (761.48bp,36.667bp) .. (14); draw (1127.5bp,241.71bp) node {g & init & r}; draw [->] (21) ..controls (787.18bp,1176.7bp) and (811.82bp,1159.1bp) .. (801.0bp,1139.1bp) .. controls (790.55bp,1119.8bp) and (769.1bp,1106.7bp) .. (10); draw (840.0bp,1146.6bp) node {g & init & !r}; draw [->] (9) ..controls (467.13bp,1184.2bp) and (451.44bp,1176.9bp) .. (437.0bp,1172.1bp) .. controls (401.59bp,1160.3bp) and (383.99bp,1177.6bp) .. (355.0bp,1154.1bp) .. controls (317.3bp,1123.6bp) and (337.63bp,1094.5bp) .. (310.0bp,1054.6bp) .. controls (305.25bp,1047.8bp) and (299.35bp,1041.1bp) .. (11); draw (388.5bp,1146.6bp) node {g & init & r}; draw [->] (6) ..controls (118.7bp,1338.6bp) and (155.32bp,1244.3bp) .. (200.0bp,1172.1bp) .. controls (211.18bp,1154.0bp) and (225.88bp,1135.6bp) .. (23); draw (194.5bp,1251.3bp) node {g & init & r}; draw [->] (13) ..controls (560.0bp,735.25bp) and (586.5bp,723.97bp) .. (609.0bp,713.17bp) .. controls (711.83bp,663.79bp) and (729.33bp,633.82bp) .. (836.0bp,593.43bp) .. controls (867.65bp,581.44bp) and (884.02bp,597.12bp) .. (910.0bp,575.43bp) .. controls (938.79bp,551.38bp) and (953.8bp,510.19bp) .. (16); draw (875.0bp,600.93bp) node {!g & init & !r}; draw [->] (20) ..controls (853.97bp,235.75bp) and (818.02bp,227.22bp) .. (798.0bp,204.21bp) .. controls (792.43bp,197.81bp) and (789.09bp,189.56bp) .. (18); draw (834.0bp,196.71bp) node {!g & init & r}; draw [->] (22) ..controls (663.73bp,928.67bp) and (604.87bp,917.06bp) .. (560.0bp,893.16bp) .. controls (545.52bp,885.44bp) and (531.57bp,873.55bp) .. (12); draw (596.0bp,885.66bp) node {!g & init & r}; draw [->] (10) ..controls (721.95bp,1120.5bp) and (721.97bp,1138.5bp) .. (725.0bp,1154.1bp) .. controls (725.68bp,1157.6bp) and (726.61bp,1161.1bp) .. (21); draw (763.0bp,1146.6bp) node {!g & init & !r}; draw [->] (11) ..controls (255.03bp,955.29bp) and (251.46bp,909.75bp) .. (272.0bp,878.16bp) .. controls (323.57bp,798.84bp) and (440.81bp,767.27bp) .. (13); draw (310.0bp,885.66bp) node {!g & init & !r}; draw [->] (17) ..controls (1139.6bp,682.22bp) and (1178.0bp,711.59bp) .. (1178.0bp,749.66bp) .. controls (1178.0bp,1679.3bp) and (1178.0bp,1679.3bp) .. (1178.0bp,1679.3bp) .. controls (1178.0bp,1710.4bp) and (1157.0bp,1715.7bp) .. (1129.0bp,1729.3bp) .. controls (1066.7bp,1759.7bp) and (858.36bp,1769.4bp) .. (3); draw (1218.5bp,1251.3bp) node {!g & !init & !r}; draw [->] (20) ..controls (969.42bp,259.7bp) and (1126.5bp,301.96bp) .. (1229.0bp,383.94bp) .. controls (1321.3bp,457.75bp) and (1384.0bp,481.77bp) .. (1384.0bp,599.93bp) .. controls (1384.0bp,1679.3bp) and (1384.0bp,1679.3bp) .. (1384.0bp,1679.3bp) .. controls (1384.0bp,1741.5bp) and (910.64bp,1766.0bp) .. (3); draw (1424.5bp,1009.8bp) node {!g & !init & !r}; draw [->] (18) ..controls (783.5bp,198.21bp) and (782.42bp,241.66bp) .. (782.0bp,279.2bp) .. controls (780.88bp,378.98bp) and (776.04bp,404.31bp) .. (785.0bp,503.68bp) .. controls (788.63bp,543.96bp) and (796.66bp,553.13bp) .. (800.0bp,593.43bp) .. controls (800.55bp,600.07bp) and (802.32bp,602.17bp) .. (800.0bp,608.43bp) .. controls (799.97bp,608.5bp) and (699.42bp,760.93bp) .. (618.0bp,803.16bp) .. controls (589.7bp,817.84bp) and (554.45bp,827.84bp) .. (12); draw (821.0bp,496.18bp) node {!g & init & r}; draw [->] (8) ..controls (409.93bp,1502.2bp) and (312.91bp,1496.9bp) .. (238.0bp,1468.3bp) .. controls (226.6bp,1464.0bp) and (225.92bp,1458.8bp) .. (215.0bp,1453.3bp) .. controls (187.24bp,1439.5bp) and (153.99bp,1427.7bp) .. (6); draw (276.0bp,1460.8bp) node {!g & init & !r}; draw [->] (5) ..controls (180.97bp,1546.6bp) and (165.84bp,1492.5bp) .. (140.0bp,1453.3bp) .. controls (135.11bp,1445.9bp) and (128.75bp,1438.8bp) .. (6); draw (211.0bp,1504.3bp) node {!g & init & !r}; draw [->] (21) ..controls (777.92bp,1209.3bp) and (786.87bp,1206.1bp) .. (786.87bp,1199.0bp) .. controls (786.87bp,1194.3bp) and (783.02bp,1191.3bp) .. (21); draw (824.87bp,1199.0bp) node {!g & init & !r}; draw [->] (10) ..controls (779.83bp,1101.5bp) and (858.94bp,1121.2bp) .. (880.0bp,1139.1bp) .. controls (902.36bp,1158.1bp) and (910.0bp,1168.6bp) .. (910.0bp,1198.0bp) .. controls (910.0bp,1679.3bp) and (910.0bp,1679.3bp) .. (910.0bp,1679.3bp) .. controls (910.0bp,1741.1bp) and (823.89bp,1762.4bp) .. (3); draw (950.5bp,1460.8bp) node {!g & !init & !r}; draw [->] (8) ..controls (433.79bp,1482.4bp) and (400.5bp,1460.1bp) .. (377.0bp,1435.3bp) .. controls (357.2bp,1414.5bp) and (361.82bp,1401.4bp) .. (341.0bp,1381.6bp) .. controls (312.95bp,1354.9bp) and (274.05bp,1333.2bp) .. (7); draw (413.0bp,1408.5bp) node {!g & init & r}; draw [->] (3) ..controls (641.39bp,1771.1bp) and (462.46bp,1763.7bp) .. (318.0bp,1729.3bp) .. controls (277.77bp,1719.8bp) and (260.31bp,1725.5bp) .. (231.0bp,1696.3bp) .. controls (210.07bp,1675.5bp) and (199.88bp,1642.5bp) .. (5); draw (269.0bp,1678.3bp) node {!g & init & !r}; draw [->] (6) ..controls (161.77bp,1441.6bp) and (250.32bp,1483.8bp) .. (253.0bp,1486.3bp) .. controls (310.46bp,1540.8bp) and (275.39bp,1595.2bp) .. (339.0bp,1642.3bp) .. controls (370.02bp,1665.3bp) and (390.47bp,1641.2bp) .. (424.0bp,1660.3bp) .. controls (442.85bp,1671.1bp) and (439.98bp,1682.9bp) .. (457.0bp,1696.3bp) .. controls (480.56bp,1715.0bp) and (487.81bp,1718.9bp) .. (516.0bp,1729.3bp) .. controls (578.07bp,1752.2bp) and (654.64bp,1764.1bp) .. (3); draw (349.5bp,1591.3bp) node {!g & !init & !r}; draw [->] (1) ..controls (110.64bp,1834.7bp) and (100.0bp,1803.4bp) .. (100.0bp,1775.2bp) .. controls (100.0bp,1775.2bp) and (100.0bp,1775.2bp) .. (100.0bp,1590.3bp) .. controls (100.0bp,1529.2bp) and (123.82bp,1513.3bp) .. (112.0bp,1453.3bp) .. controls (111.31bp,1449.8bp) and (110.34bp,1446.3bp) .. (6); draw (138.0bp,1634.8bp) node {!g & init & !r}; draw [->] (9) ..controls (520.15bp,1210.3bp) and (530.0bp,1207.3bp) .. (530.0bp,1199.0bp) .. controls (530.0bp,1193.5bp) and (525.76bp,1190.3bp) .. (9); draw (566.0bp,1199.0bp) node {!g & init & r}; draw [->] (15) ..controls (659.84bp,371.55bp) and (658.31bp,377.96bp) .. (657.0bp,383.94bp) .. controls (638.46bp,468.53bp) and (653.68bp,495.23bp) .. (621.0bp,575.43bp) .. controls (617.37bp,584.33bp) and (613.95bp,585.18bp) .. (609.0bp,593.43bp) .. controls (581.99bp,638.41bp) and (553.73bp,692.72bp) .. (13); draw (677.0bp,548.55bp) node {!g & init & !r}; draw [->] (3) ..controls (670.46bp,1767.6bp) and (597.35bp,1757.2bp) .. (542.0bp,1729.3bp) .. controls (527.29bp,1721.9bp) and (513.23bp,1710.0bp) .. (4); draw (568.5bp,1721.8bp) node {!g & !init}; draw [->] (19) ..controls (1215.2bp,522.27bp) and (1223.3bp,513.12bp) .. (1229.0bp,503.68bp) .. controls (1242.3bp,481.93bp) and (1306.0bp,313.18bp) .. (1306.0bp,287.7bp) .. controls (1306.0bp,287.7bp) and (1306.0bp,287.7bp) .. (1306.0bp,143.34bp) .. controls (1306.0bp,75.619bp) and (794.21bp,44.214bp) .. (14); draw (1339.5bp,286.7bp) node {g & init & r}; draw [->] (0) ..controls (243.11bp,1945.2bp) and (212.9bp,1934.7bp) .. (189.0bp,1921.1bp) .. controls (173.46bp,1912.2bp) and (157.62bp,1899.9bp) .. (1); draw (227.0bp,1913.6bp) node {!g & init & !r}; draw [->] (23) ..controls (209.69bp,1023.6bp) and (148.64bp,941.37bp) .. (185.0bp,878.16bp) .. controls (248.62bp,767.55bp) and (424.49bp,752.79bp) .. (13); draw (223.0bp,885.66bp) node {!g & init & !r}; draw [->] (12) ..controls (435.74bp,836.39bp) and (324.99bp,828.06bp) .. (299.0bp,803.16bp) .. controls (164.11bp,673.97bp) and (210.0bp,579.22bp) .. (210.0bp,392.44bp) .. controls (210.0bp,392.44bp) and (210.0bp,392.44bp) .. (210.0bp,143.34bp) .. controls (210.0bp,72.631bp) and (452.34bp,45.508bp) .. (14); draw (243.5bp,443.81bp) node {g & init & r}; draw [->] (17) ..controls (1082.9bp,615.89bp) and (1083.6bp,603.15bp) .. (1090.0bp,593.43bp) .. controls (1101.2bp,576.47bp) and (1113.4bp,583.68bp) .. (1132.0bp,575.43bp) .. controls (1139.4bp,572.15bp) and (1147.2bp,568.56bp) .. (19); draw (1128.0bp,600.93bp) node {!g & init & !r}; draw [->] (16) ..controls (889.02bp,415.77bp) and (763.79bp,372.88bp) .. (15); draw (872.0bp,391.44bp) node {!g & init & r}; draw [->] (9) ..controls (510.1bp,1169.2bp) and (523.37bp,1150.2bp) .. (540.0bp,1139.1bp) .. controls (588.13bp,1107.1bp) and (656.19bp,1095.4bp) .. (10); draw (576.0bp,1146.6bp) node {g & init & !r}; draw [->] (13) ..controls (523.57bp,691.52bp) and (524.61bp,596.41bp) .. (549.0bp,521.68bp) .. controls (551.75bp,513.27bp) and (623.81bp,391.11bp) .. (629.0bp,383.94bp) .. controls (633.17bp,378.18bp) and (637.98bp,372.29bp) .. (15); draw (586.0bp,548.55bp) node {!g & init & r}; draw [->] (7) ..controls (280.35bp,1281.7bp) and (366.12bp,1254.0bp) .. (437.0bp,1225.8bp) .. controls (447.6bp,1221.6bp) and (459.1bp,1216.5bp) .. (9); draw (425.0bp,1251.3bp) node {!g & init & r}; draw [->] (16) ..controls (1002.3bp,549.6bp) and (1082.0bp,800.25bp) .. (1082.0bp,884.66bp) .. controls (1082.0bp,1088.9bp) and (1082.0bp,1088.9bp) .. (1082.0bp,1088.9bp) .. controls (1082.0bp,1117.9bp) and (1080.5bp,1125.2bp) .. (1083.0bp,1154.1bp) .. controls (1090.8bp,1244.2bp) and (1115.0bp,1264.6bp) .. (1115.0bp,1355.1bp) .. controls (1115.0bp,1679.3bp) and (1115.0bp,1679.3bp) .. (1115.0bp,1679.3bp) .. controls (1115.0bp,1749.3bp) and (868.38bp,1767.5bp) .. (3); draw (1123.5bp,1146.6bp) node {!g & !init & !r}; draw [->] (2) ..controls (517.09bp,1579.7bp) and (540.61bp,1569.9bp) .. (557.0bp,1555.3bp) .. controls (604.18bp,1513.4bp) and (615.42bp,1496.0bp) .. (633.0bp,1435.3bp) .. controls (659.19bp,1345.0bp) and (561.55bp,1253.5bp) .. (9); draw (674.0bp,1408.5bp) node {!g & init & r}; draw [->] (3) ..controls (689.58bp,1745.6bp) and (652.05bp,1721.5bp) .. (623.0bp,1696.3bp) .. controls (591.62bp,1669.1bp) and (593.53bp,1651.8bp) .. (560.0bp,1627.3bp) .. controls (544.9bp,1616.3bp) and (525.75bp,1607.5bp) .. (2); draw (659.0bp,1678.3bp) node {!g & init & r}; draw [->] (18) ..controls (830.19bp,159.25bp) and (856.7bp,170.95bp) .. (874.0bp,189.21bp) .. controls (880.25bp,195.8bp) and (884.86bp,204.44bp) .. (20); draw (921.0bp,196.71bp) node {g & init & !r}; draw [->] (11) ..controls (284.99bp,962.71bp) and (301.71bp,931.15bp) .. (325.0bp,911.16bp) .. controls (368.53bp,873.81bp) and (434.54bp,855.08bp) .. (12); draw (361.0bp,938.03bp) node {!g & init & r}; draw [->] (7) ..controls (230.03bp,1333.9bp) and (233.91bp,1341.4bp) .. (237.0bp,1348.6bp) .. controls (253.01bp,1385.8bp) and (236.93bp,1406.1bp) .. (265.0bp,1435.3bp) .. controls (281.08bp,1452.1bp) and (292.44bp,1444.8bp) .. (314.0bp,1453.3bp) .. controls (329.73bp,1459.6bp) and (333.08bp,1462.6bp) .. (349.0bp,1468.3bp) .. controls (379.89bp,1479.4bp) and (416.19bp,1489.7bp) .. (8); draw (303.0bp,1408.5bp) node {!g & init & !r}; draw [->] (18) ..controls (713.45bp,222.75bp) and (558.32bp,390.04bp) .. (545.0bp,398.94bp) .. controls (526.41bp,411.38bp) and (510.68bp,398.52bp) .. (498.0bp,416.94bp) .. controls (431.89bp,513.06bp) and (486.44bp,663.73bp) .. (13); draw (537.0bp,443.81bp) node {!g & init & !r}; draw [->] (21) ..controls (771.17bp,1224.0bp) and (780.12bp,1233.5bp) .. (786.0bp,1243.8bp) .. controls (799.37bp,1267.3bp) and (801.0bp,1275.7bp) .. (801.0bp,1302.7bp) .. controls (801.0bp,1461.8bp) and (801.0bp,1461.8bp) .. (801.0bp,1461.8bp) .. controls (801.0bp,1489.4bp) and (800.43bp,1498.9bp) .. (815.0bp,1522.3bp) .. controls (821.67bp,1533.1bp) and (831.59bp,1528.9bp) .. (837.0bp,1540.3bp) .. controls (839.85bp,1546.4bp) and (838.27bp,1548.8bp) .. (837.0bp,1555.3bp) .. controls (821.16bp,1637.2bp) and (806.88bp,1656.1bp) .. (767.0bp,1729.3bp) .. controls (764.32bp,1734.2bp) and (761.2bp,1739.3bp) .. (3); draw (855.5bp,1504.3bp) node {!g & !init & !r}; draw [->] (6) ..controls (129.92bp,1418.8bp) and (138.87bp,1415.6bp) .. (138.87bp,1408.5bp) .. controls (138.87bp,1403.8bp) and (135.02bp,1400.8bp) .. (6); draw (176.87bp,1408.5bp) node {!g & init & !r}; draw [->] (8) ..controls (493.29bp,1488.0bp) and (505.99bp,1478.8bp) .. (515.0bp,1468.3bp) .. controls (543.42bp,1435.2bp) and (532.92bp,1415.0bp) .. (561.0bp,1381.6bp) .. controls (580.36bp,1358.6bp) and (607.68bp,1338.0bp) .. (24); draw (597.0bp,1408.5bp) node {g & init & !r}; draw [->] (12) ..controls (545.54bp,832.62bp) and (590.44bp,825.81bp) .. (629.0bp,821.16bp) .. controls (649.61bp,818.68bp) and (800.17bp,817.69bp) .. (815.0bp,803.16bp) .. controls (904.96bp,715.0bp) and (802.32bp,639.07bp) .. (848.0bp,521.68bp) .. controls (851.58bp,512.49bp) and (857.35bp,512.85bp) .. (861.0bp,503.68bp) .. controls (892.72bp,424.14bp) and (896.76bp,321.26bp) .. (20); draw (885.0bp,548.55bp) node {g & init & !r}; draw [->] (1) ..controls (226.21bp,1853.5bp) and (583.35bp,1798.6bp) .. (3); draw (489.5bp,1826.6bp) node {!g & !init & !r}; draw [->] (22) ..controls (807.74bp,934.7bp) and (934.0bp,921.14bp) .. (934.0bp,841.66bp) .. controls (934.0bp,841.66bp) and (934.0bp,841.66bp) .. (934.0bp,599.93bp) .. controls (934.0bp,476.96bp) and (911.46bp,331.52bp) .. (20); draw (970.0bp,600.93bp) node {g & init & !r}; draw [->] (0) ..controls (260.58bp,1889.7bp) and (228.09bp,1739.4bp) .. (303.0bp,1660.3bp) .. controls (343.71bp,1617.3bp) and (382.09bp,1668.9bp) .. (435.0bp,1642.3bp) .. controls (447.85bp,1635.9bp) and (459.3bp,1624.7bp) .. (2); draw (297.0bp,1774.2bp) node {!g & init & r}; draw [->] (24) ..controls (688.9bp,1266.5bp) and (705.82bp,1245.3bp) .. (21); draw (744.0bp,1251.3bp) node {!g & init & !r}; draw [->] (7) ..controls (202.55bp,1230.3bp) and (194.41bp,1130.2bp) .. (226.0bp,1054.6bp) .. controls (228.95bp,1047.6bp) and (233.55bp,1040.9bp) .. (11); draw (237.5bp,1199.0bp) node {g & init & r}; draw [->] (14) ..controls (489.39bp,52.994bp) and (313.0bp,90.057bp) .. (313.0bp,143.34bp) .. controls (313.0bp,751.66bp) and (313.0bp,751.66bp) .. (313.0bp,751.66bp) .. controls (313.0bp,820.61bp) and (418.0bp,835.65bp) .. (12); draw (349.0bp,443.81bp) node {!g & init & r}; draw [->] (0) ..controls (362.0bp,1923.2bp) and (610.51bp,1824.9bp) .. (3); draw (564.5bp,1870.1bp) node {!g & !init}; draw [->] (21) ..controls (686.83bp,1170.9bp) and (632.98bp,1145.3bp) .. (612.0bp,1139.1bp) .. controls (506.72bp,1108.2bp) and (377.51bp,1095.9bp) .. (23); draw (680.5bp,1146.6bp) node {g & init & r}; draw [->] (19) ..controls (1225.3bp,568.95bp) and (1241.3bp,579.92bp) .. (1252.0bp,593.43bp) .. controls (1269.5bp,615.42bp) and (1275.0bp,624.2bp) .. (1275.0bp,652.3bp) .. controls (1275.0bp,1679.3bp) and (1275.0bp,1679.3bp) .. (1275.0bp,1679.3bp) .. controls (1275.0bp,1735.5bp) and (1213.3bp,1715.2bp) .. (1159.0bp,1729.3bp) .. controls (1020.1bp,1765.6bp) and (848.17bp,1772.1bp) .. (3); draw (1315.5bp,1199.0bp) node {!g & !init & !r}; draw [->] (15) ..controls (700.81bp,405.61bp) and (738.65bp,498.24bp) .. (719.0bp,575.43bp) .. controls (690.57bp,687.11bp) and (681.55bp,727.06bp) .. (595.0bp,803.16bp) .. controls (576.64bp,819.31bp) and (550.34bp,828.7bp) .. (12); draw (751.0bp,600.93bp) node {!g & init & r}; draw [->] (19) ..controls (1179.3bp,586.22bp) and (1174.0bp,598.93bp) .. (1166.0bp,608.43bp) .. controls (1154.9bp,621.59bp) and (1138.7bp,631.69bp) .. (17); draw (1212.0bp,600.93bp) node {g & init & !r}; draw [->] (15) ..controls (718.79bp,315.05bp) and (763.26bp,295.23bp) .. (802.0bp,279.2bp) .. controls (824.21bp,270.02bp) and (849.64bp,260.18bp) .. (20); draw (838.0bp,286.7bp) node {g & init & !r}; draw [->] (17) ..controls (1153.1bp,652.16bp) and (1216.3bp,645.23bp) .. (1252.0bp,608.43bp) .. controls (1303.0bp,555.9bp) and (1282.3bp,341.55bp) .. (1244.0bp,279.2bp) .. controls (1221.3bp,242.32bp) and (1204.7bp,239.56bp) .. (1165.0bp,222.21bp) .. controls (1046.5bp,170.39bp) and (891.83bp,153.05bp) .. (18); draw (1313.0bp,391.44bp) node {!g & init & r}; draw [->] (5) ..controls (132.7bp,1551.3bp) and (9.981bp,1459.0bp) .. (58.0bp,1381.6bp) .. controls (83.761bp,1340.1bp) and (139.39bp,1320.3bp) .. (7); draw (98.0bp,1460.8bp) node {!g & init & r}; draw [->] (16) ..controls (1003.9bp,454.15bp) and (1012.9bp,450.92bp) .. (1012.9bp,443.81bp) .. controls (1012.9bp,439.15bp) and (1009.0bp,436.16bp) .. (16); draw (1050.9bp,443.81bp) node {!g & init & !r}; draw [->] (13) ..controls (486.11bp,741.74bp) and (455.89bp,732.17bp) .. (437.0bp,713.17bp) .. controls (417.08bp,693.13bp) and (413.0bp,682.55bp) .. (413.0bp,654.3bp) .. controls (413.0bp,654.3bp) and (413.0bp,654.3bp) .. (413.0bp,495.18bp) .. controls (413.0bp,458.81bp) and (403.24bp,450.41bp) .. (389.0bp,416.94bp) .. controls (385.42bp,408.52bp) and (381.37bp,407.78bp) .. (379.0bp,398.94bp) .. controls (372.22bp,373.67bp) and (378.0bp,366.24bp) .. (378.0bp,340.07bp) .. controls (378.0bp,340.07bp) and (378.0bp,340.07bp) .. (378.0bp,143.34bp) .. controls (378.0bp,65.679bp) and (489.69bp,43.296bp) .. (14); draw (412.5bp,391.44bp) node {g & init & r}; draw [->] (12) ..controls (529.22bp,849.98bp) and (538.5bp,847.36bp) .. (538.5bp,840.66bp) .. controls (538.5bp,836.37bp) and (534.69bp,833.75bp) .. (12); draw (574.5bp,840.66bp) node {!g & init & r}; draw [->] (1) ..controls (73.273bp,1855.2bp) and (0.0bp,1828.4bp) .. (0.0bp,1775.2bp) .. controls (0.0bp,1775.2bp) and (0.0bp,1775.2bp) .. (0.0bp,1407.5bp) .. controls (0.0bp,1330.2bp) and (115.02bp,1311.0bp) .. (7); draw (36.0bp,1591.3bp) node {!g & init & r}; % end{tikzpicture} } }](eqs/vu8p1e45srbnb-280.png)
A PDF of the automaton is available here. Note that the graph only shows the colors of some of the states (next to the state numbers), but there are still four different colors, as in the previous automaton. Also, the sink state (from which all suffix words are rejected) is missing from the automaton. The new automaton looks a lot more complicated even though the specification is still quite simple. While at least one other LTL-to-parity-automaton tool produces a smaller automaton for this specification, note that pretty much all automata that encode interesting specifications are quite large, which explains why real-world examples of parity automata are seldomly found in the literature.
At this point, I would like to thank Alexandre Duret-Lutz for helpful suggestions on using spot to generate parity automata.
Ok, What's Their Use Now?
Deterministic parity automata can encode specifications of reactive systems, just like temporal logic formulas or other automaton types over words of infinite length (such as Büchi automata that almost every student taking a formal methods course learns about). Once a specification has been formalized, it can be used in automatic procedures for the verification and/or synthesis of reactive systems.
For probabilistic systems, there is frequently the question of how large the probability is to satisfy (or violate) a specification. Non-deterministic automata cannot be used for this purpose (for reasons whose discussion would lead beyond the scope of this page), but rather deterministic automata have to be used. Parity automata are the simplest automaton model that can capture all
 -regular acceptance conditions, and are hence a natural choice.
-regular acceptance conditions, and are hence a natural choice.In the field of reactive synthesis, we automatically synthesize a finite-state implementation from a formal specification. Again, the use of non-deterministic automata to represent the specification is problematic (as discussed in Section 4.2.3 of my PhD thesis), but deterministic automata can be used by translating the automaton to a parity game while splitting up the alphabet into input and output. The parity game can then be analyzed by a game solving algorithm. When done right, a winning strategy for the player choosing the output values is a reactive system implementation that always satisfies the specification, no matter what input the environment provives to the reactive system.




